Binary Positive to Negative
Invert all the bits and add one:
0101 => 5 1010 + 1 ---- 1011 => -5
Binary Negative to Positive
Invert all the bits and add one:
1011 => -5 0100 + 1 ---- 0101 => 5
Binary Negative to Decimal
Consider the highest-order bit as having a negative weight and all other bits as having a positive weight:
1011 => -1*2^3 + 0*2^2 + 1*2^1 + 1*2^0
=> -8 + 0 + 2 + 1
=> -5
Unsigned Complements
Thinking in terms of unsigned n-bit integers, the two's complement of x is always given by 2^n - x. For example, for 4-bit numbers:
2^4 - 5 = 16 - 5 = 11 [1011] 2^4 - 11 = 16 - 11 = 5 [0101]
In a 4-bit world the two's complement of 5 is 11 and the two's complement of 11 is 5. A number and its complement always sum to 2^n.
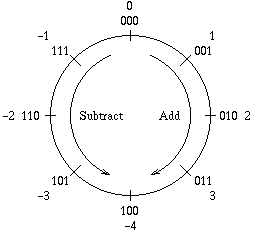
Range
An n-bit two's complement integer can represent the range from –2n-1 to 2n-1 – 1. For example, a 3-bit two's complement integer can represent the range from –22 to 22 – 1, i.e. from –4 to 3, as illustrated below: